Geometrisch nichtlineare Probleme in der Statik (Master)
Dieses Master-Modul ist konzipiert als ein Überblick über das breite Themenfeld der geometrisch nichtlinearen Theorie - insbesondere bei Stab- und Flächentragwerken – und der entsprechenden kontinuumsmechanischen Grundlagen.
Nach einer detaillierten Einführung in die Theorie 2. Ordnung für eben belastete Stabsysteme folgt die Erweiterung auf den räumlich belasteten Stab (auf Dehnung, zweiachsige Biegung und Torsion). Eine exemplarische FE-Formulierung eines 3D-Stabelementes mit geometrischer Nichtlinearität demonstriert die Umsetzung der Theorie und verdeutlicht die Behandlung von Instabilitätsphänomenen. Als zwei weitere geometrisch nichtlineare Problemklassen werden das linearisierte Plattenbeulen und das Durchschlagproblem betrachtet. Die theoretischen Grundlagen der geometrisch nichtlinearen Theorie werden durch eine kompakte Einführung in die Kontinuumsmechanik dargestellt. Hierbei werden Verzerrungstensoren als quadratische Verzerrungsmaße mit Erfassung großer Verschiebungen und Rotationen definiert – und in Beziehung zu den arbeitskonformen Spannungen gesetzt. Der Zusammenhang der geometrisch nichtlinearen Betrachtung mit Instabilitätsphänomenen wird theoretisch und anhand von Rechenbeispielen mit Stab- und Schalenmodellen verdeutlicht. Die Lösungstechniken für geometrisch nichtlineare Probleme werden anhand von klassischen Lösungsverfahren (Newton-Raphson) und am Beispiel einer Pfadverfolgungsprozedur vermittelt.
Alle numerischen Übungsbeispiele werden mit Hilfe von MATLAB® oder in ANSYS® realisiert. Die Studierenden werden dazu befähigt, praktische Lösungen für geometrisch nichtlineare Problemstellungen unter Verwendung von FE-basierter Software und Computer-Algebra-Systemen zu entwickeln.
Auf einen Blick
- Einführung: Problemstellungen in der nichtlinearen Statik
- Der Biegestab nach Theorie 2. Ordnung: Stabilitätsfaktoren, geometrisch nichtlineare Stabsteifigkeitsmatrizen – exakte Lösung und FE-Formulierung; iterative Lösungen mit MATLAB / ANSYS
- Finite Rotationen im 3D-Kontinuum: mathematische Beschreibung der Rotation, finite und moderate Rotationswinkel
- Geometrische Nichtlinearität bei 3D-Stabsystemen: räumlich belasteter Stab, Differentialgleichungen, freie Torsion / Wölbkrafttorsion; Instabilitätsfälle - Behandlung nach Eurocode 3
- Plattenbeulen: die Kirchhoff‘sche Plattentheorie nach Theorie 2. Ordnung; das Kippen als räumliches Instabilitätsproblem
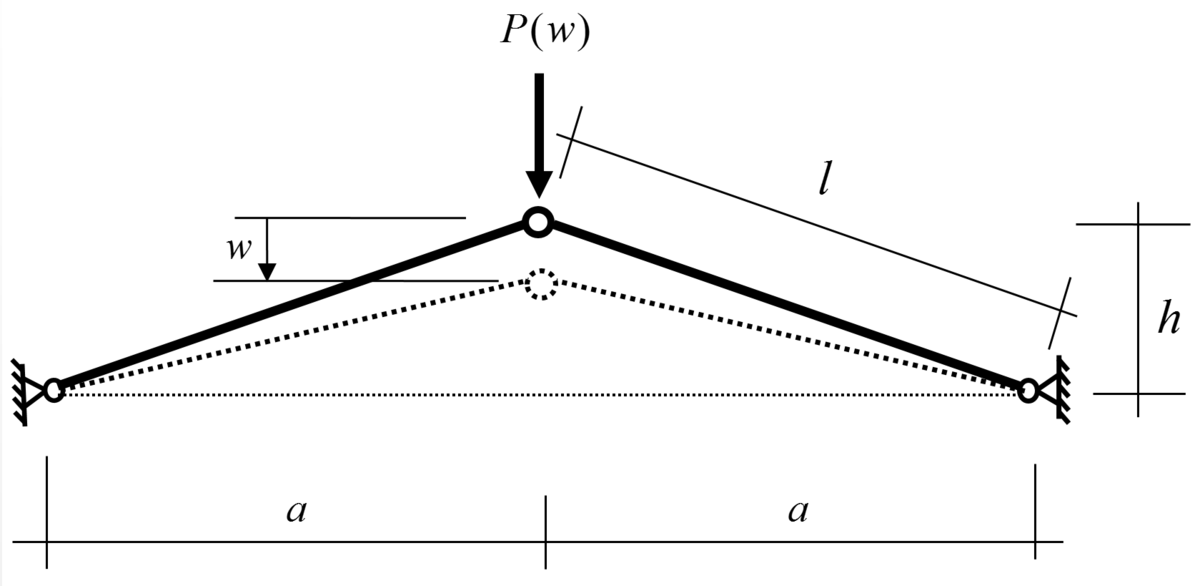
- Das Durchschlagproblem: analytische MATLAB-Lösung; kinetische Betrachtung des Durchschlagens
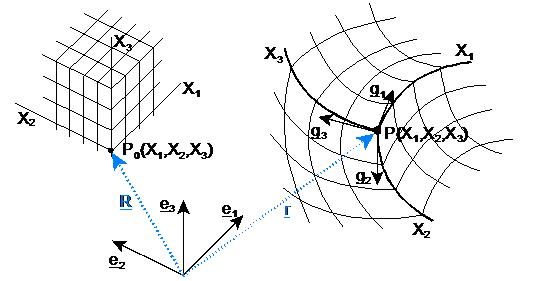
- Grundlagen der Kontinuumsmechanik: Definition der Konfigurationen, geometrische Verformungsbeschreibung, nichtlineare Kinematik für große Verschiebungen und Rotationen, Definitionen der Verzerrungstensoren, Spannungstensoren
- Stabilitätsprobleme und Pfadverfolgungsverfahren: die Gleichgewichtsverzweigung, stabile und labile Gleichgewichtszustände, Verzweigungsaufgaben mit ANSYS, Pfadverfolgungsverfahren zur Lösung nichtlinearer Aufgaben