Geometric Non-Linear Problems in Statics (Master’s)

This master’s level module is designed to provide an introduction to the broad subject area of geometric non-linear theory, with particular reference to beam and plate structures, and the concomitant fundamentals of the continuum mechanics.

A detailed introduction to 2^nd order theory for in-plane loaded beam systems is followed by a study of the spatially loaded beam (subjected to axial deformation, bi-axial bending and torsion). The example of a finite element formulation of a 3D beam element with geometric non-linearity is used to demonstrate the practical application of the theory and the management of instability phenomena. Two additional problem classes on the geometric non-linear theory are considered in the form of linearised plate buckling and the snap-through buckling. The fundamental theoretical principles of geometric non-linear theory are presented in the form of a compact introduction to continuum mechanics. This involves the definition of strain tensors as quadratic strain measures in conjunction with large displacements and rotations and are placed in relation to the work-conform stresses. The links between the non-linear geometric approach and instability phenomena are explained theoretically and on the basis of computational examples in conjunction with beam and shell models. The solution methods for geometric non-linear problems are taught with reference to classic solution methods (Newton-Raphson) and using the example of a path tracing procedure.

All numerical example exercises are performed using MATLAB® or ANSYS®. Students learn how to solve geometric non-linear problems with the use of finite element based software and computer algebra systems.

• Introduction: Defining the subject in Non-Linear Statics
• The Beam Model According to the Theory of the 2^nd Order: Stability factors, geometric non-linear beam stiffness matrices – precise solutions and finite element formulation; iterative solutions with MATLAB / ANSYS
• Finite rotations in 3D continuum: mathematical description of the rotation, finite and moderate rotation angle
• Geometric Non-linearity in 3D frame systems: spatially loaded beam, differential equations, free torsion / warping torsion; instability cases - treatment in compliance with Eurocode 3
• Plate buckling: the Kirchhoff plate theory by 2^nd order theory; lateral-torsional buckling as a spatial instability problem
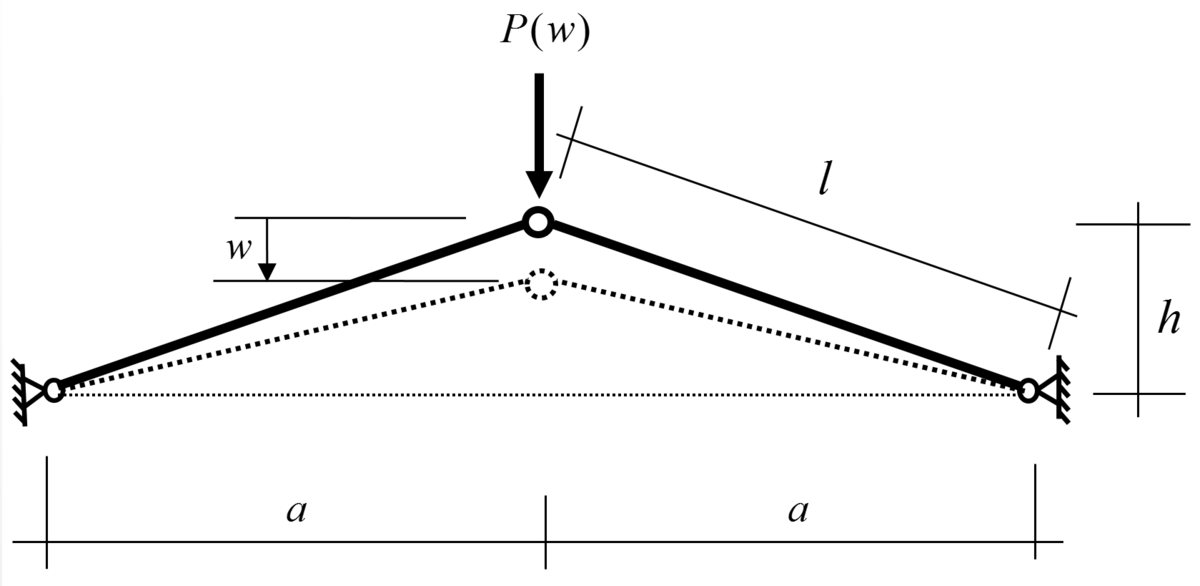
• The snap-through problem: analytical MATLAB solution; the snap-through buckling as a kinetic problem
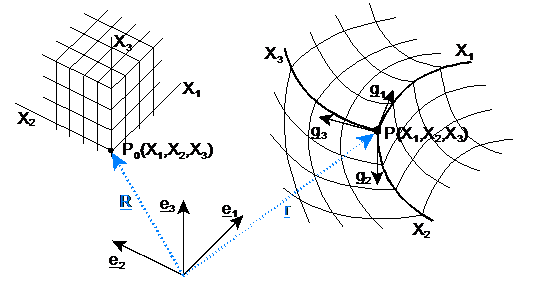
• Elementary continuum mechanics: Defining the configurations, geometric deformations, non-linear kinematics for large deflections and rotations, strain tensors and stress tensors
• Stability problems and path tracing methods: the bifurcation of equilibrium, stable and non-stable equilibrium states, bifurcation problems with ANSYS, path tracing procedures for solving non-linear problems